Единицы измерения длины
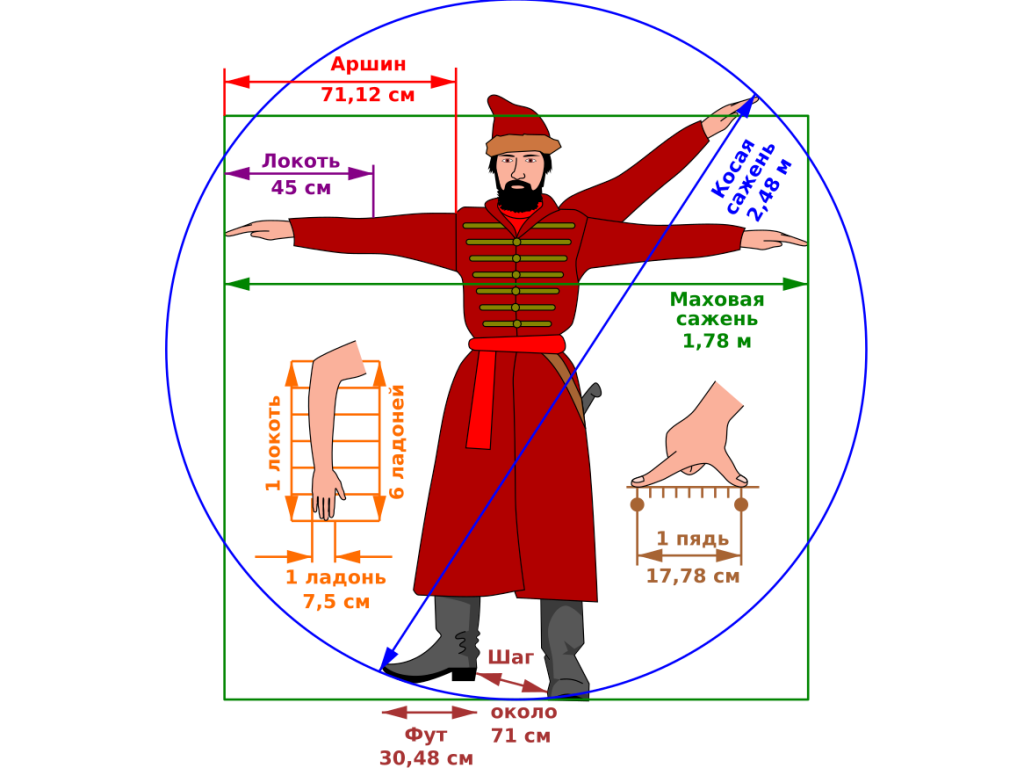
В старину длины различных предметов измеряли с помощью всевозможных линеек с нанесенными на них особыми единицами измерения. У каждого государства были свои мерки. Например, старорусский инструмент для измерения длины назывался аршин. Но длина этой линейки была неодинаковой в разных регионах. Даже пословица возникла «Мерить на свой аршин». Другое название этой меры – шаг (приблизительно 71 см).
Такое различие мешало торговле, и люди договорились измерять длины с помощью метровой линейки, эталон которой хранится в штаб-квартире Международного бюро мер и весов близ Парижа (Франция). Каждое государство имеет копии этой метровой линейки, с которых, в свою очередь, снимаются копии всех линеек страны.
Для удобства метр поделили на 10 равных частей, получили новую единицу измерения длины – дециметр (десятая часть метра). Потом дециметр тоже поделили на 10 равных частей, получили сантиметр (сотая часть метра). Далее сантиметр поделили на 10 равных частей и получили миллиметр (тысячная часть метра).
«Мили» переводится с латинского как «тысяча» Латинские корни имеют также приставки санти – «сто» и деци – «десятый».
Приставка кило- имеет древнегреческое происхождение и означает «тысяча».
Измерение длин отрезков. Периметр
Когда мы измеряем длину отрезка, мы сравниваем его со шкалой линейки. Сколько сантиметров или миллиметров могло бы расположиться на отрезке, такова и его длина.
Чтобы найти длину ломаной, необходимо сложить длины всех звеньев, составляющих её.
Замкнутая ломаная линия представляет собой многоугольник, если её звенья не пересекаются. В этом случае звенья называют сторонами, а длину ломаной называют периметром многоугольника.
Слово периметр сложилось из латинских слов пери – «вокруг», «кругом» и метр – «мера».
Формула периметра прямоугольника
Четырехугольник, у которого углы прямые, называют прямоугольником. Он обладает интересным свойством: у него противоположные стороны имеют равные длины. Это свойство позволяет упростить вычисление его периметра.
Рассмотрим прямоугольник ABCD. Чтобы найти его периметр сложим длины всех его сторон:
AB + BC + CD + DА.
Пусть в нём две противоположные стороны имеют длину а:
AB = CD = а,
а две другие стороны длину b:
BC = DА = b.
Тогда длина периметра будет:
а + b + а + b = (а + а) + (b + b) = 2 · а + 2 · b или
а + b + а + b = (а + b) + (а + b) = 2 · (а + b), где а + b – сумма длин двух соседних сторон и называется полупериметр.
Значит, периметр прямоугольник можно найти удвоением суммы длин двух его соседних сторон.
Это и есть формула периметра прямоугольника:
2 · (а + b).
Например, если одна сторона прямоугольника имеет длину а = 3 см, а другая b = 5 см, то у такого прямоугольника периметр будет равен:
2 · (а + b) = 2 · (3 см + 5 см) = 16 см.
Распределительный закон умножения
Из вывода формулы периметра прямоугольника можно заметить, что
2 · (а + b) = 2 · а + 2 · b.
Оказывается это равенство справедливо для любых чисел а, b и с, то есть: с · (а + b) = с · а + с · b.
И называют это равенство распределительным законом умножения относительно сложения. То есть множитель с как бы распределяется (раздаётся) по всем слагаемым в скобках.
Чтобы число умножить на сумму двух чисел, надо это число умножить на каждое слагаемое и полученные произведения сложить.
Справедливо и обратное равенство: с · а + с · b = с · (а + b).
Запоминалочка
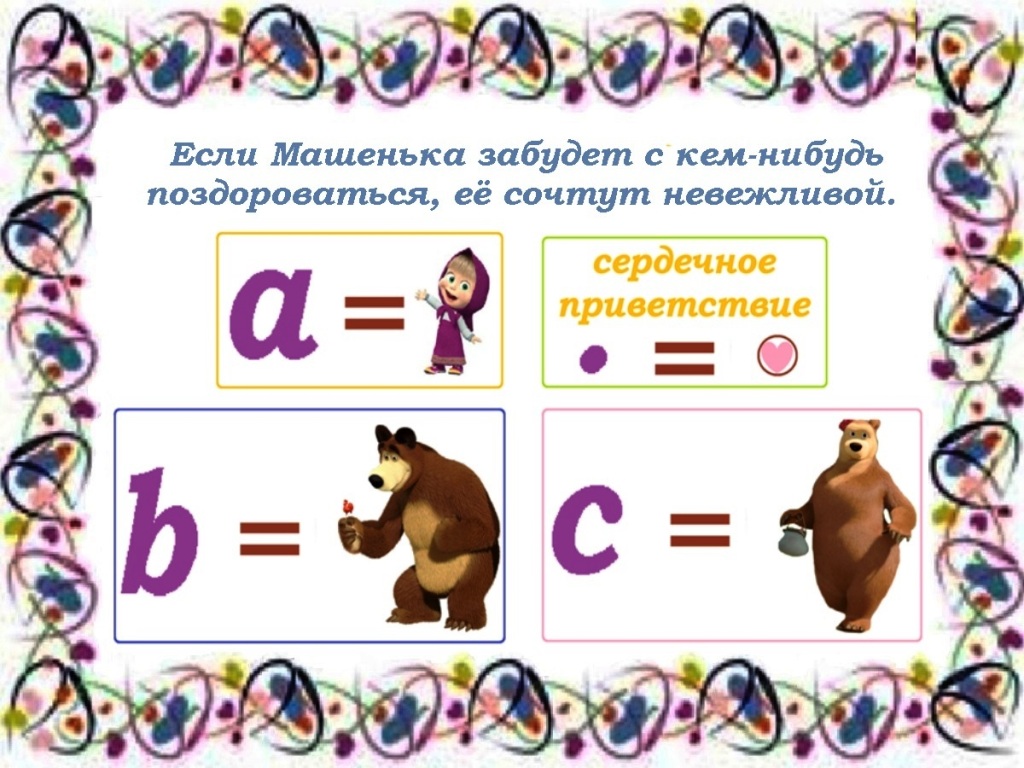
Запомнить это равенство поможет этикет.
Перепишем закон в другой форме:
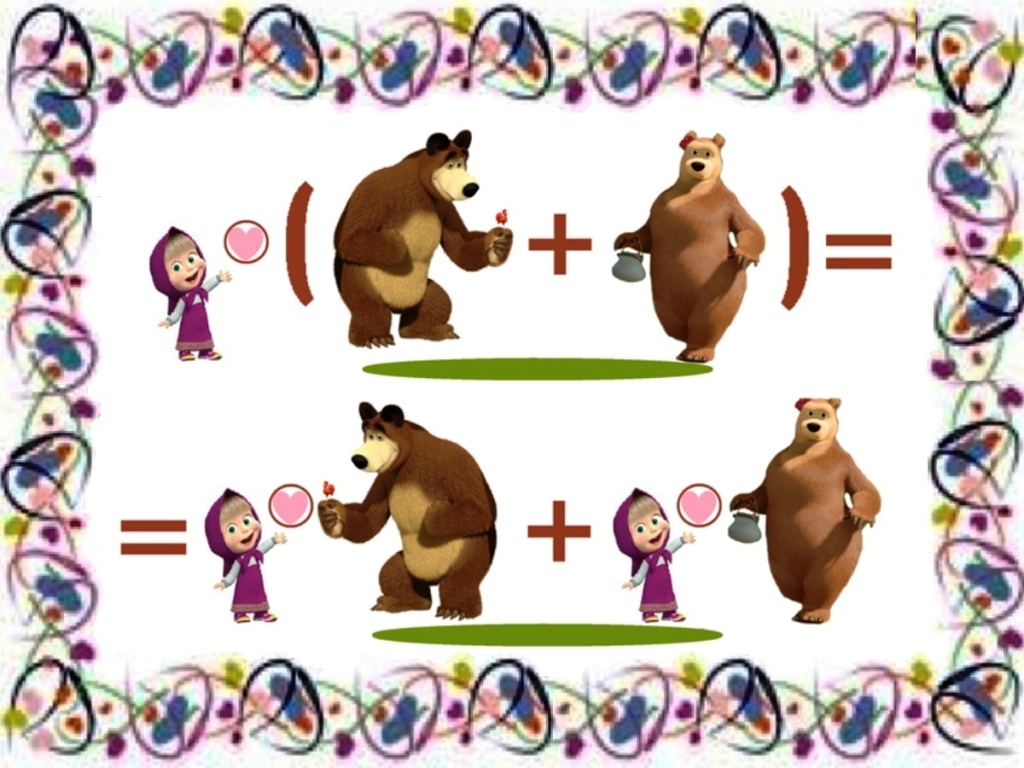
а · (b + с) = а · b + а · с.
Если знак умножения представить как рукопожатие, то вежливый человек а, придя в гости к b и к с поздоровается как с хозяином b, так и с хозяйкой с.